Datums (061.01.03.01)
Define ‘true north’ (TN) (…03.01.01)
Measure a true direction on any given aeronautical chart (…03.01.02)
Define ‘magnetic north’ (MN) (…03.01.03)
Define and apply variation (…03.01.04)
Explain changes of variation with time and position (…03.01.05)
Define ‘compass north’ (CN) (…03.01.06)
Apply deviation (…03.01.07)
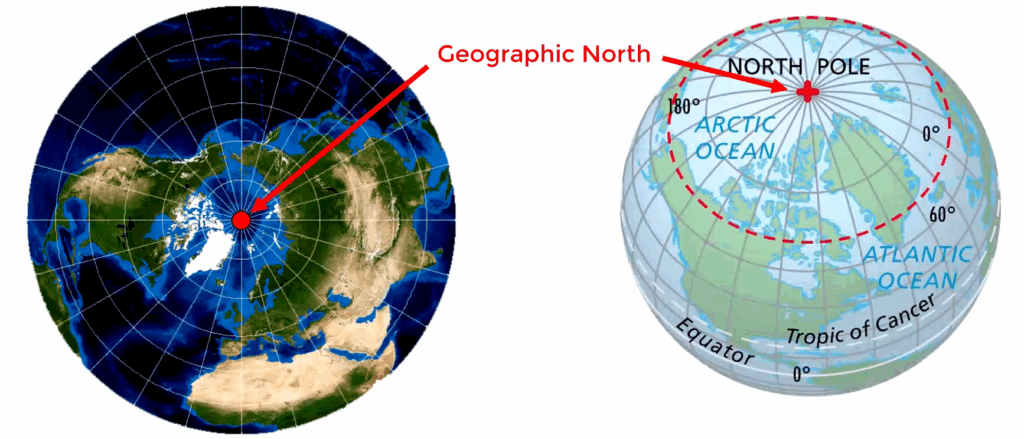
Direction in navigation is measured as an angle from a datum. On Earth the datum for direction is the geographic North Pole. This is the point where the Earth’s axis of rotation meets its surface. Directions are measured in degrees in a clockwise direction from the north datum, the so called “True North (TN)“. True directions are shown with the letter T after the degrees sign, like: 035°T.
It is possible to read true directions straight of an aeronautical chart, by aligning the protractor with the True North reference, the meridians.
In flight, compasses are used to find direction, and compasses indicate the direction with reference to the Earth’s magnetic pole, not the geographic pole. The magnetic pole is the point through which the magnetic field lines re-enter the planet.
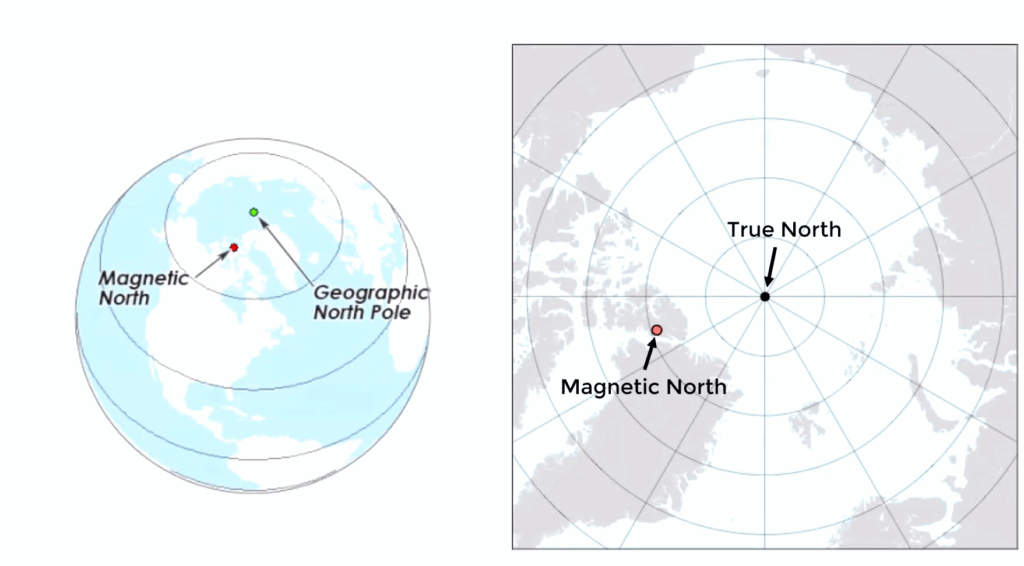
The magnetic pole is not at the same location as the geographic pole. Actually, this magnetic pole is not even fixed and changes position over time due to fluctuations in the Earth’s magnetic field. (Currently, Magnetic North is located in the Arctic region, near Canada, and is moving towards Siberia.)
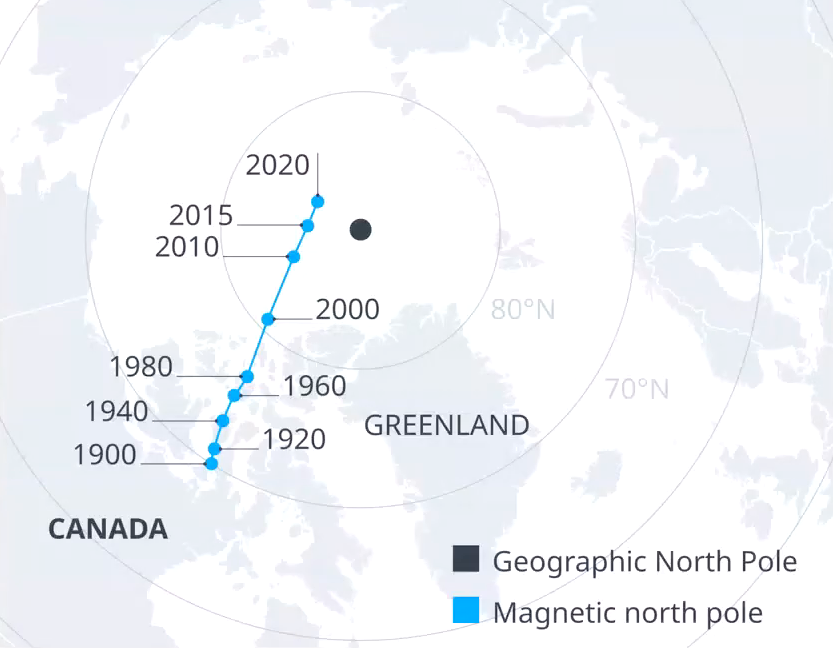
While the True North is a fixed point, Magnetic North (MN) varies, as stated, over time and varies based on the geographical location as the Earth’s magnetic field is not uniform.The difference is referred to as Magnetic Variation.
Magnetic Direction
Variation is the difference between True and Magnetic heading.
Variation is measured in degrees, and is named east or west according to whether the Magnetic North lies to the east or west of the True North at a specific point.
So magnetic heading, plus or minus variation, equals true heading. Whether to “add” or to “subtract” is depending on whether the MN is west or east of the TN at a certain location.
- East variation: MN is east of TN, in this case you should subtract the variation from the True North.
- West variation: MN is west of TN, in this case you should add the variation to the True North.
Mnemonic:
Variation east, magnetic least (-)
Variation west, magnetic best (+)
Important: Variation can be given like, 4°W or 16°E. But also like: -4° or +16°, which is exactly the same. So in those cases read + as east, and – as west.
Mnemonic (rewritten):
Variation east (+), magnetic least (-)
Variation west (-), magnetic best (+)
Compass Direction
The readings of the Earth’s magnetic field by a compass installed in an airplane is distorted by the surrounding metal and electrical equipment. The needle slightly deviates from magnetic north and indicates a direction known as the Compass North (C).
Deviation is the difference between Compass North and Magnetic North.
Deviation is also measured in degrees and is one again described as east (+), west (-).
Mnemonic :
Deviation east (+), compass least (-)
Deviation west (-), compass best (+)
Calculations
In order to convert an aircraft’s compass heading to a true heading and vice versa, deviation and variation has to be applied in the correct sequence. Using this table might help:
| C (compass) | D (deviation) | M (magnetic) | V (variation) | T (true) |
|---|
Example 1: Given, true heading is 005°, variation 32°„, deviation 4°E. What is the compass heading?
}
Solution:
| C | D | M | V | T |
|---|---|---|---|---|
| 4°E | 32°W | 005° |
First apply variation to the True heading to find the Magnetic heading. Variation west, magnetic best, so we have to add the variation to find the Magnetic heading.
005° + 32° = 037°
| C | D | M | V | T |
|---|---|---|---|---|
| 4°E | 037° | 32°W | 005° |
Now apply the variation. Deviation East, compass least, so we have to subtract the deviation to find the Compass heading.
037° – 4° = 033°
Example 2: Given, compass heading is 233°, true heading 246°„, deviation -3°. What is the variation?
}
Solution:
| C | D | M | V | T |
|---|---|---|---|---|
| 233° | -3° (3°W) | ? | ? | 246° |
Note: -3° means 3°W. So Magnetic heading + 3°W = 233° (Compass heading). Magnetic heading is therefore 230° (233° – 3°).
| C | D | M | V | T |
|---|---|---|---|---|
| 233° | -3° (3°W) | 230 | ? | 246° |
246° (T) – 16° (V) = 230° (M). So we have subtracted the variation, and as east is least, the variation in this case is 16°E or +16°.
Richting in navigatie wordt gemeten als een hoek ten opzichte van een referentiepunt.
Track and heading (061.01.03.02)
Calculate XWC by: trigonometry; and MDR. (…03.02.01)
Explain and apply the concepts of drift and WCA (…03.02.02)
Calculate the actual track with appropriate data of heading and drift (…03.02.03)
Calculate TKE with appropriate data of WCA and drift (…03.02.04)
Calculate the heading change at an off-course fix to directly reach the next waypoint using the 1:60 rule (…03.02.05)
Calculate the average drift angle based upon an off-course fix observation (…03.02.06)
Crosswind Component
The crosswind component (XWC) is the portion of the wind that blows perpendicular to the aircraft’s runway or flight path.
Calculation of the XWC can be done either by trigonometry, the CSRP-5 and by Mental Dead Reckoning .
Trigonometry
The standard formula: XWC = V×sin(θ)
Where:
V = wind speed
θ = angle between the wind direction and the (runway) heading.
Example: Given the following information, using trigonometry, calculate the crosswind component (XWC), to the nearest knot.
Runway: 32
Wind (magnetic): 020°/25 kt
Solution:
Aligned with runway 32, and assume it is heading 320°M. The wind is from 020°M, which is 60° to our right.
XWC = 25kt x sin(60°) = 22kt.
Memory aid: “Soh Cah Toa”
CRP-5
Place the center dot over the top-line of the bottom grid (crosswind grid). St the wind direction of 020° under the True Heading Index.
Mark the wind speed of 25kt right under the center dot.
Set the track of 320°under the True Index and read a XWC of ±22kt.
Mental Dead Reckoning
Mental Dead Reckoning is the process of using mental rules of thumb to estimate a value. So, using MDR does not guarantee the exact same answer as using trigonometry.
Two MDR techniques for estimating the XWC,
- The “Clock Code” rule:
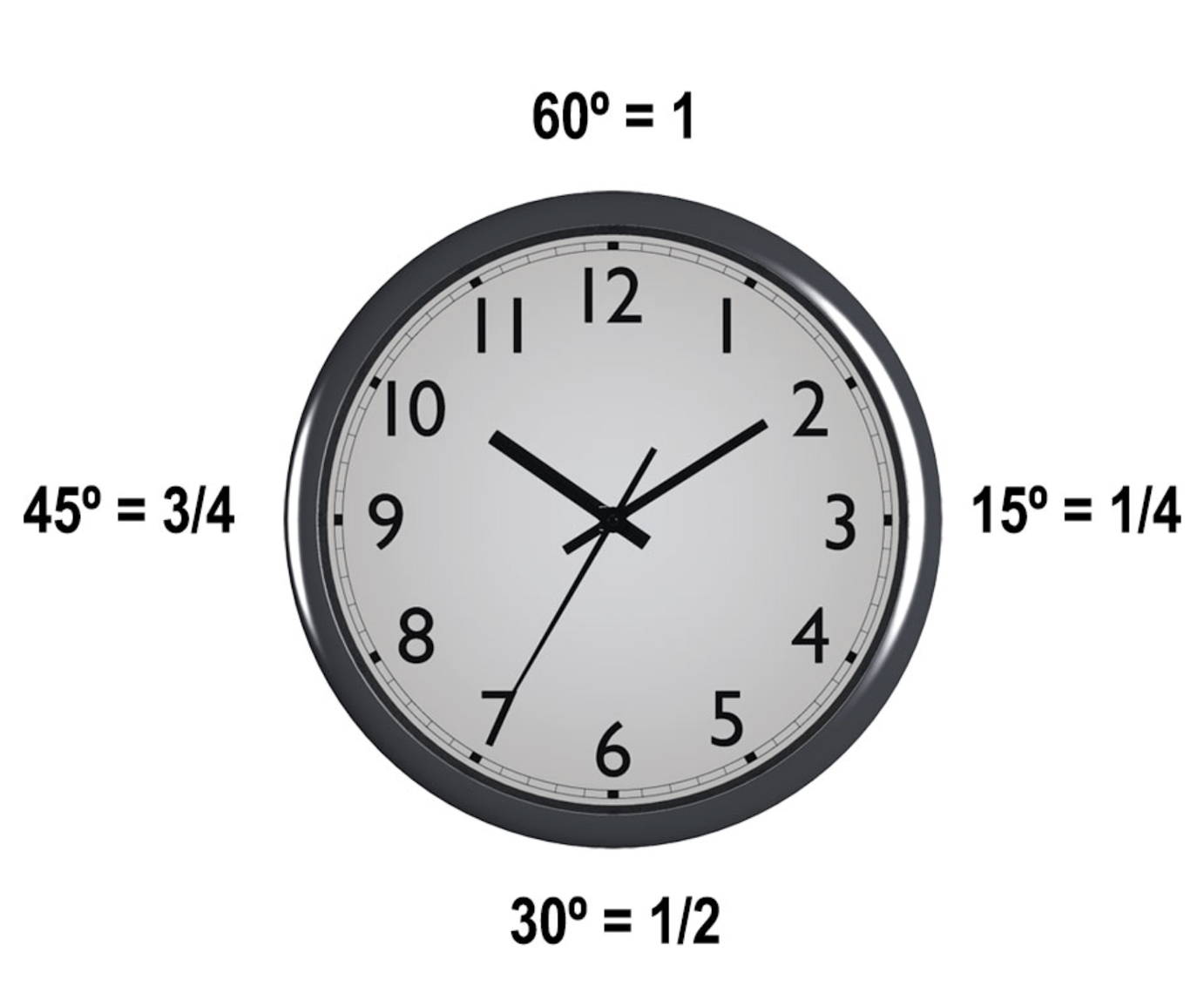
- Table:
| Wind Angle | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
|---|---|---|---|---|---|---|---|---|---|---|
| Aid | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | 2 | 1 |
| Multiply wind speed by: | 0 | 0.2 | 0.3 | 0.5 | 0.6 | 0.8 | 0.9 | 0.9 | 1 | 1 |
To help with the construction of this table EASA recommends an “aid”, with the sequence 11, 22, 33. The idea is to add 1 to 10, add 1 to 20, add 2 to 30, add 2 to 40, add 3 to 50, add 3 to 60, see the second row of the table.
Example 1: What is the value of the crosswind on your heading and which way is it blowing you, given the parameters:
TAS 250 KTS
HDG 080° (T)
TRK 090° (T)
GS 290 KTS
Solution:
Make a quick schematic drawing of the situation, to determine the Drift.
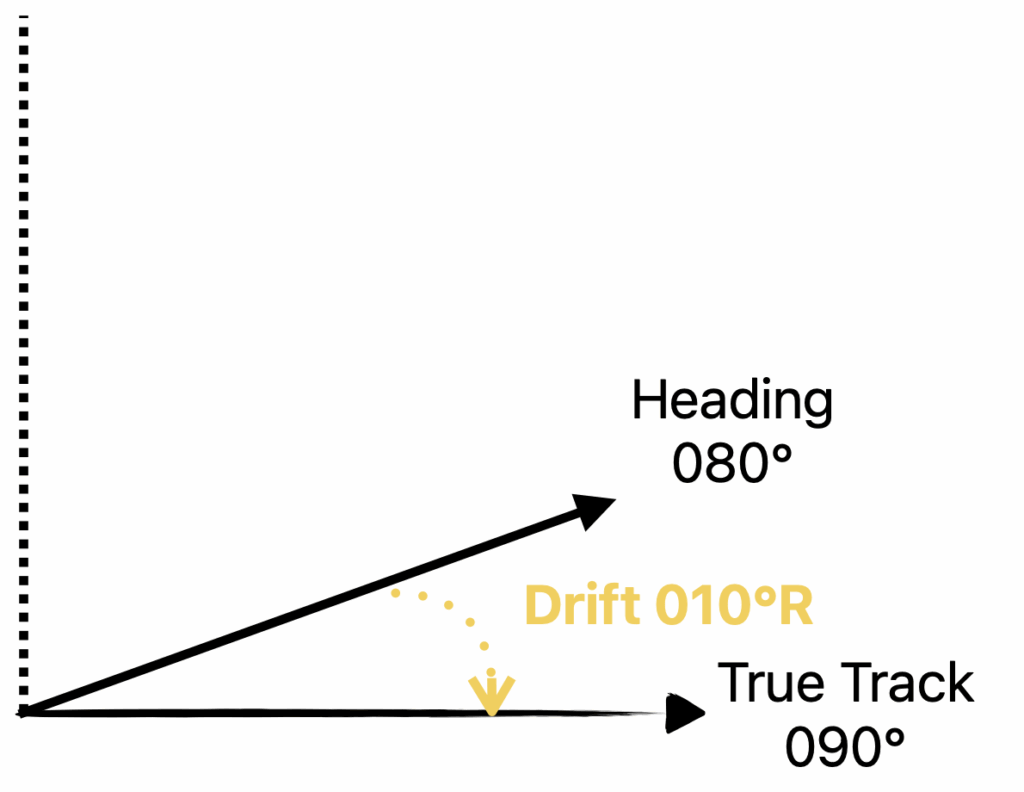
Drift is from Heading to Track so in this case 10° Right.
| Air | Ground |
| Heading 080°(T) TAS 250 kt | Track 090°(T) GS 290kt |
Step 1: set the center dot at the TAS of 250kt;
Step 2: put the heading of 080° under the True Heading Index.
Step 3: place a small wind-mark at the intersection of 10°R drift and the ground speed of 290kt.
Step 4: rotate the inner-circle until the wind-marker is on the centerline right under the center dot.
Now, under the True Heading Index it reads the wind direction: ± 312°(T). And the distance between the center dot and the wind-mark shows the velocity of the wind: ± 62kt.
We are not completely done yet, as they are asking “what is the value of the crosswind on your heading and which way is it blowing you…“.
CRP-5
Step 1: rotate the inner-circle back to the heading of 080°(T).
Note: The wind-mark should be back at the intersection of 10°R drift and GS 290kt.
Step 2: move the slide, until the wind-mark is on the top line of the crosswind grid at the bottom of the slide.
Step 3: count across from the center-line to the wind-marker, it shows a crosswind of ± 49kt.
Note: The difference between the center-dot and the top of the crosswind-grid shows the tailwind component.
Trigonometry
θ , the angle between the wind (312°) direction and the heading (080°) is 312 – 80 – 180 = 53°.
XWC = 62kt x sin(53°) = 49kt.
Heading, Track and Drift
The heading of an aircraft is the direction the airplane’s nose is pointing, measured as an angle from the north (T, M or C).
The track is the aircraft’s path over the ground, of which we distinguish two:
- Required track, the track we wish to follow;
- Track made good, the actual track;
Track Error (TKE), is the angle between the required track and the track made good.
Drift, is the angle between the aircraft heading and the track made good (actual).
Drift is expressed as to the left (port) or to the right (starboard). Where, important to remember, drift goes from heading to track (air to actual).
Drift goes from heading to track (air to actual).
Wind Correction Angle
If there is wind hitting the airplane, let’s say, from the left, and we don’t compensate for it, then it will push (drift) the plane to the right. So with the same heading, the actual track will be drifted to the right of the required track.
In order to maintain the required track, we have to compensate for the wind, by pointing the noise of the plane slightly into the wind. Actually, by the same angle as the drift would have been, but in opposite direction. This what is called the Wind Correction Angle (WCA).
So the WCA applied to the required track, gives the required heading to be flown. For example:
| Required Track | 156° |
| WCA | 7°L |
| Heading | 149° |
or:
| Required Track | 156° |
| Drift | 7°R |
| Heading | 149° |
Calculate the actual track with appropriate data of heading and drift (…03.02.03)
Example: Given the following information, determine the actual track of the aircraft.
Planned track: 157°(T)
Pre-flight wind correction angle calculation: 8° left
Actual in-flight drift: 10° right.
Solution:
The pre-flight WCA of 8° left, implies that they were expecting a 8° right drift. So by heading 149°(T), 8° to the left of the planned track of 157°(T), they would have counter acted on the 8° right drift.
However the actual in-flight drift was 10° right, so they were experiencing an additional drift of 2°. This means the actual track was 159°(T) and not 157°(T).
Calculate the heading change at an off-course fix to directly reach the next waypoint using the 1:60 rule
Track Error Angle (TKE) = (Distance off track x 60) / Distance gone.
Track Error Angle (TKE) = (Distance off track x 60) / Distance to go.
Example 1: A VFR flight is navigated by dead reckoning. Flying from B to C, the position of the aircraft is fixed and a change of heading calculated. The 1:60 rule is used to determine the heading from the fix position to be back on track in approximately the same time it has taken from B to the fix position. Using the following information, what heading is required?
Planned DR heading from B to C: 313°C
Cross track error: 3 NM left
Along track distance from B: 45 NM
Solution:
The along track distance from “B” was 45 NM when the TKE was noticed, so the distance gone is 45NM. The distance of track given is 3NM (left).
TKE = (Distance off track x 60) / Distance gone = (3NM x 60)/45 = 4°.
So we have to turn 4° to the right (as the cross track error was left), to parallel the indented track.
Now in order to turn in the direction of “C” we have another 45NM to go (based on this sentence “in approximately the same time it has taken from B to the fix position”).
TKE = (Distance off track x 60) / Distance to go = (3NM x 60)/45 = 4°.
So we need to turn another 4* to the right to head for position “C”: 313° + 4° + 4° = 321°(C).