Speed (061.01.05)

Different air speeds are considered in aviation:

Indicated Airspeed (IAS) is what the airspeed indicator (ASI) reads. But that reading doesn’t always reflect what’s actually happening outside the aircraft. Enter Calibrated, True, Equivalent, and Groundspeed. Think of them like different camera lenses on the same aircraft, each shows a slightly different angle, and together, they give you the full picture:

IAS helps you obey speed limits and fly by the book.

CAS adjusts for minor instrument or installation errors.

EAS becomes important at higher speeds where compressibility of air matters.

TAS tells you your actual speed through the air mass, crucial for navigation and flight planning.

GS is your real-world travel speed over the ground, affected by wind.

Calibrated Airspeed

Calibrated Airspeed (CAS) is IAS corrected for instrument and position error. Or, in other words, it is the airspeed that should be after correcting inaccuracies in the airspeed indicator itself and disruptions in airflow around the static and pitot ports.

For most modern training aircraft in straight and level flight, IAS and CAS are nearly the same, differences are usually within 1–2 knots. However, during slow flight, steep climbs, or slips/skids, the difference becomes more pronounced.

Equivalent Airspeed

EAS = CAS corrected for compressibility effects.

While Calibrated Airspeed (CAS) is accurate enough at lower speeds and altitudes, once you start climbing higher and approaching transonic speeds, compressibility begins to affect accuracy. That’s when EAS becomes relevant.

In general aviation flying below 200 KTAS and under 10,000 feet, EAS is rarely a practical concern.

True Airspeed (TAS)

The Speed You’re Really Flying

True Airspeed (TAS) is your actual speed through the air mass, how fast you’re moving relative to the surrounding air. It is CAS corrected for non-standard air density, which means adjusting for altitude and temperature.

As altitude increases, the air gets thinner (lower pressure and density). For the same CAS, you’re moving through more air molecules per second at low altitudes than at high ones. So even though your CAS might read the same, your TAS is higher the higher you go.

Why TAS Matters?

• TAS is used to calculate groundspeed and estimated time enroute.

Source: airheadatpl.com

Calculations

Considering the learning objective “Calculate TAS from CAS, and CAS from TAS by: mechanical computer”:

---

Example 1: Calculate the TAS of an aircraft flying at FL150, where the temperature is -15°C at a CAS of 150kt.

Solution:

Using the CRP-5 computer:

Step 1: in the AIRSPEED window, align the “pressure altitude x 1000”, thus 15, with the OAT of –15°C (be aware of the plus and minus temperature scale).

Step 2: on the inner scale find the CAS of 150kt (15). Now read the TAS on the outer scale against the CAS of ± 189kt (18,1).

---

Example 2: Determine the CAS, given the following information:

TAS: 180 kt 
Pressure altitude: ​FL​120 
Temperature: ​I​SA +20​ºC

Solution:

The outside air temperature (OAT) according to ISA, is 15°C (sea level) – 2°C / 1000ft, so at FL120 (12,000ft) the ISA outside air temperature should be 15*C – 24°C = – 9°C . But the question states that the OAT is actually 20°C higher, so 11°C.

Now using the CRP-5 computer:

Step 1: in the AIRSPEED window, align the “pressure altitude x 1000”, thus 12, with the OAT of +11°C (be aware of the plus and minus temperature scale).

Step 2: on the outer scale find the TAS of 180kt (18). Now read the CAS on the inner scale against the TAS of ± 145kt (14,5).

The rule of thumb “Add 2% to CAS for every 1,000 feet above sea level.“, provides an equal answer: CAS + (12×2%)CAS = CAS + 0.24CAS =1.24CAS =TAS. CAS = TAS / 1.24 = 180/1.24 ≈ 145.

---

Compressibility correction

At higher altitudes and speeds, in fact when the TAS exceeds 300KT, there will be a correction required for a compressibility error.

Compressibility correction applied above 300KT TAS.

In order to apply a correction, divide the TAS by 100 and subtract 3 (formula is on the computer). This will result in a division which you apply in the COMP. CORR. window, in the direction of the arrow.

Always turn in the direction of the arrow!

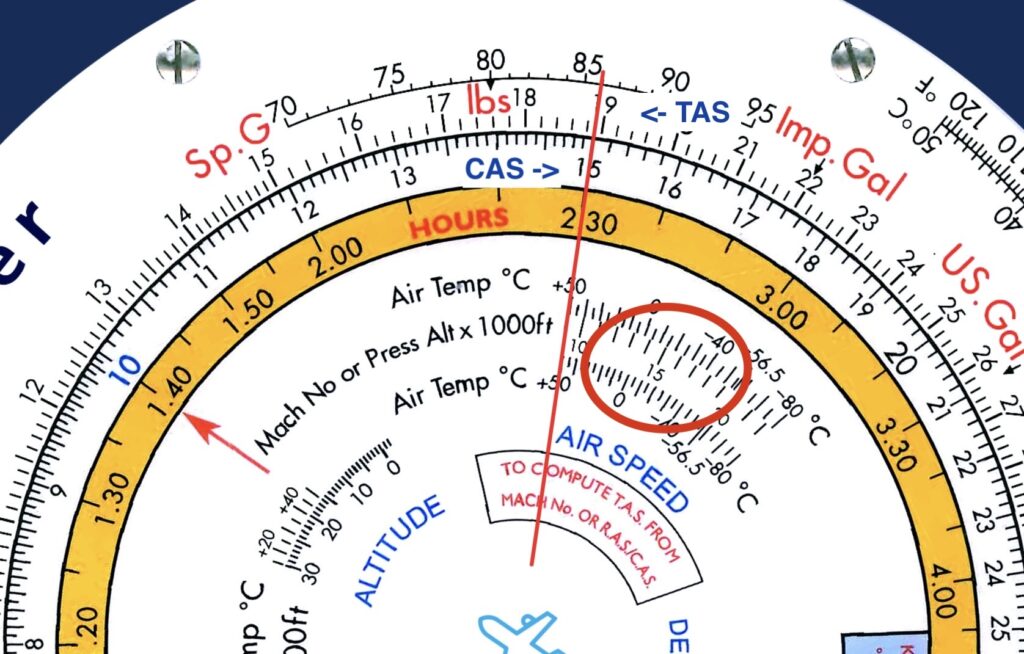
Example 1: Calculate the TAS of aircraft flying at FL300 where the temperature is -56.5°C at a CAS of 280kt.

Solution:

Step 1: in the AIRSPEED window align the pressure altitude (30) with the temperature of -56.5°C.

Step 2: on the inner-scale find the CAS of 280kt (28) and read the TAS aligned on the outer-scale, 440kt.

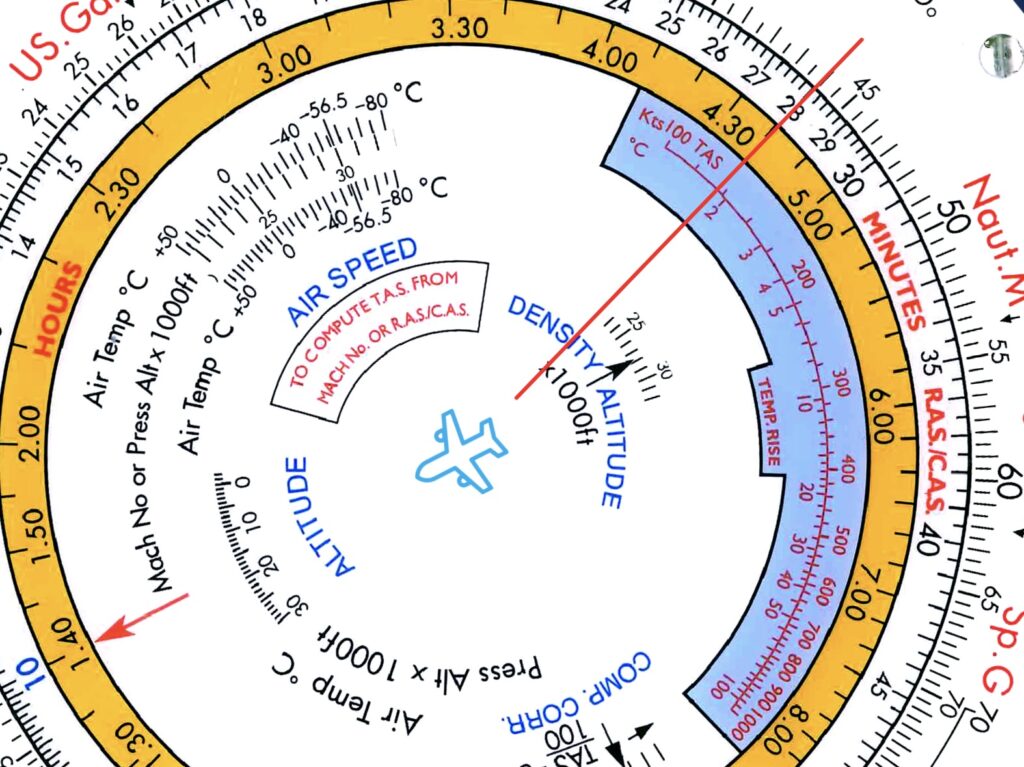
Now that the TAS of 440kt is larger than 300kt, we have to make a compressibility correction of (440/100)-3 = 1.4 divisions.

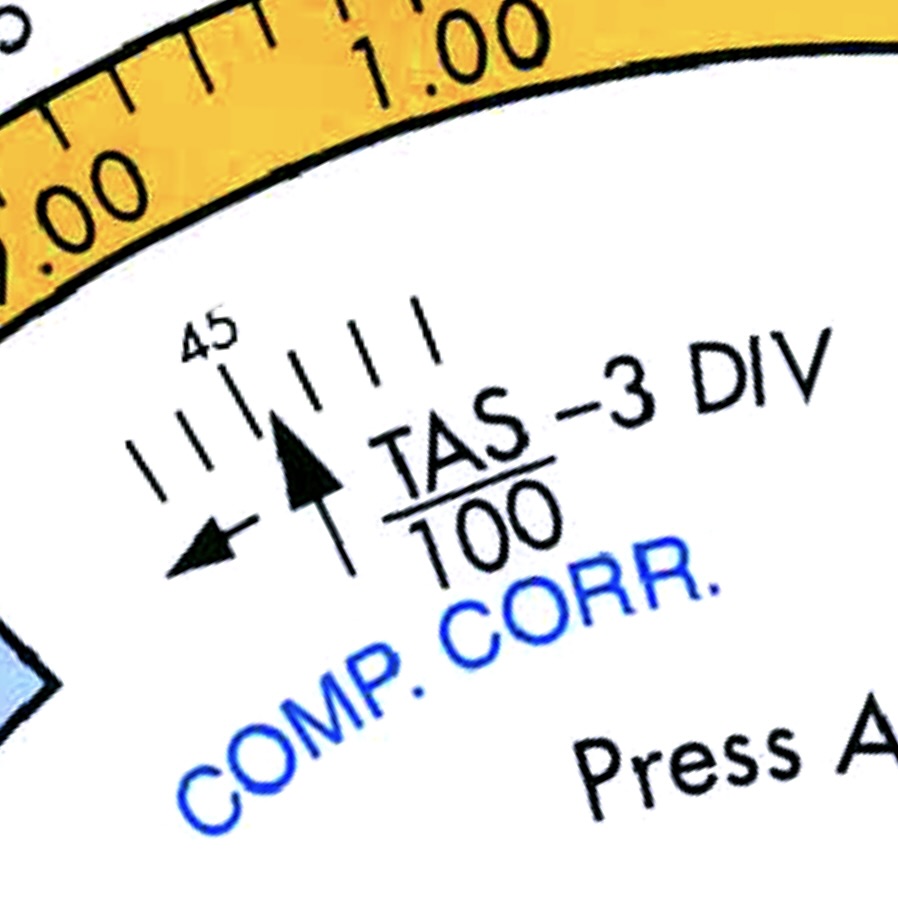
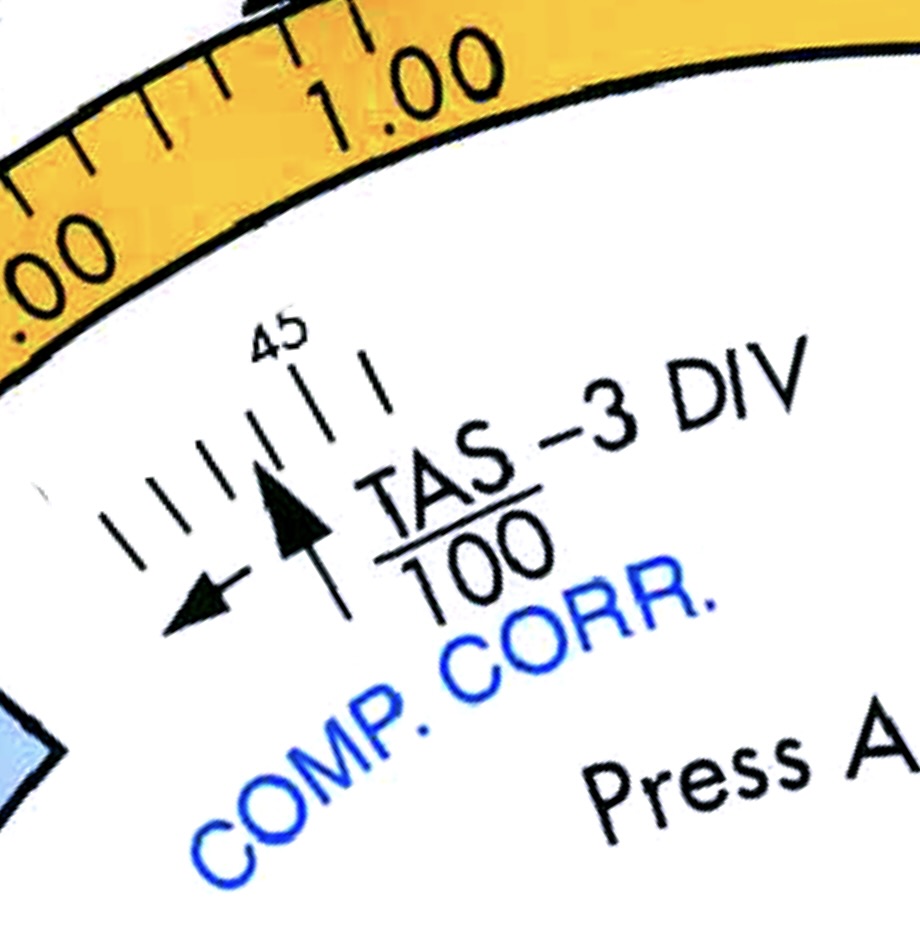
Step 3: in the COMP. CORR window turn 1.4 divisions towards the arrow.

Step 4: return to the inner-scale and fint the CAS of 280kt (28) again, and read the TAS aligned on the outer-scale, ±436kt.

So after correction the TAS is not 440kt but 436kt.

Mach number (061.01.05.02)

Calculate TAS from M, and M from TAS. (…05.02.01)

The Mach number is a proportion of the airspeed in relation to the Local Speed of Sound (LSS).

Above Mach 1, faster than the local speed of sound, an aircraft flies supersonic. If the aircraft is flying at Mach 0.8, it is traveling at 80% of the local speed of sound.

For navigation purposes we need to be able to convert from Mach to TAS and back again. The relationship between Mach and TAS mathematically:

Mach = TAS / LSS

The local speed of sound varies with temperature. It can be calculated mathematically:

LSS = 38.94 x √T °A

A constant of 38.94 multiplied by the square root of the outside air temperature in degrees absolute.

Note: absolute zero (0°A) equals -273°C, and 0°C = 273°A.

Calculations

Example 1: calculate the Mach number given a TAS of 360kt and an OAT of -25°C.

Solution:

Step 1: in the “AIR SPEED”-window align the Mach No. Index with the air temperature of -25°Ç.

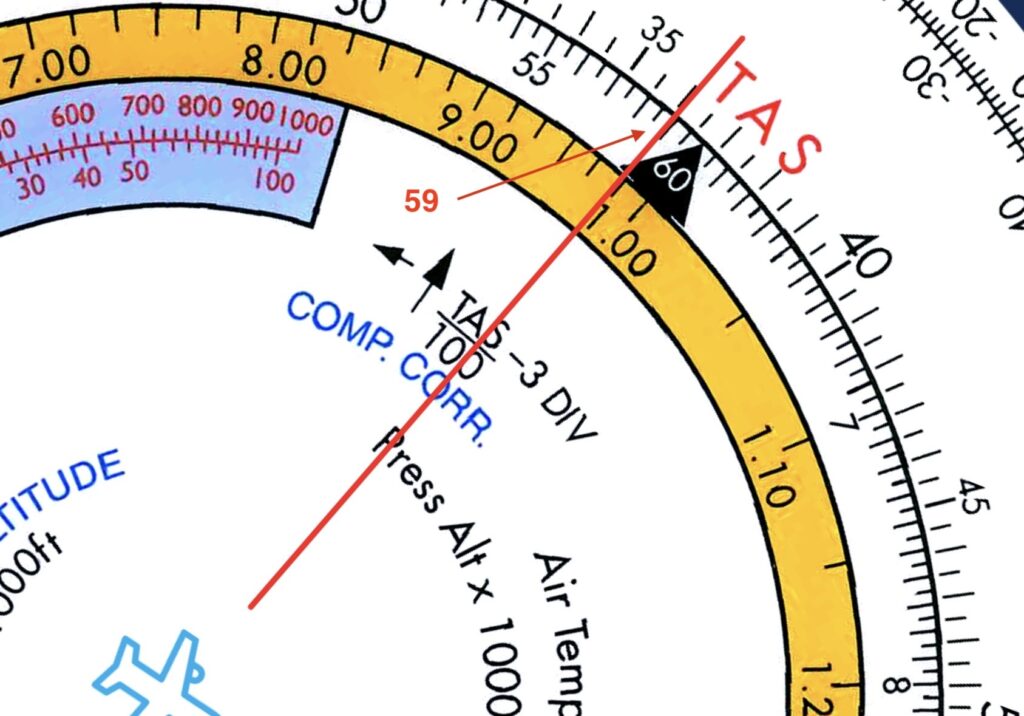
Step 2: on the outer-scale lookup the TAS of 360 kt (36) and read the aligned Mach No.± 0.59 on the outer-scale

Or when not using the CRP-5, you could calculate the Mach No. as follows:

273°A = 0°Ç, so -25°Ç = 273°A – 25° = 248*A (absolute).

Local Speed of Sound (LSS) = 38.94 x √248°A = 613.22.

Mach No = TAS / LSS = 360/613.22 = 0.587.

---

Example 2: What is the TAS of an aircraft flying at Mach number 0.85 at FL400 where the outside temperature is ISA +10*C.

Solution:

The OAT is 10°C warmer than it would have been according to the International Standard Atmosphere, which at FL400 (tropopause) is a constant of -56.5°C. So the current OAT is -46.5°Ç (-56.5 + 10).

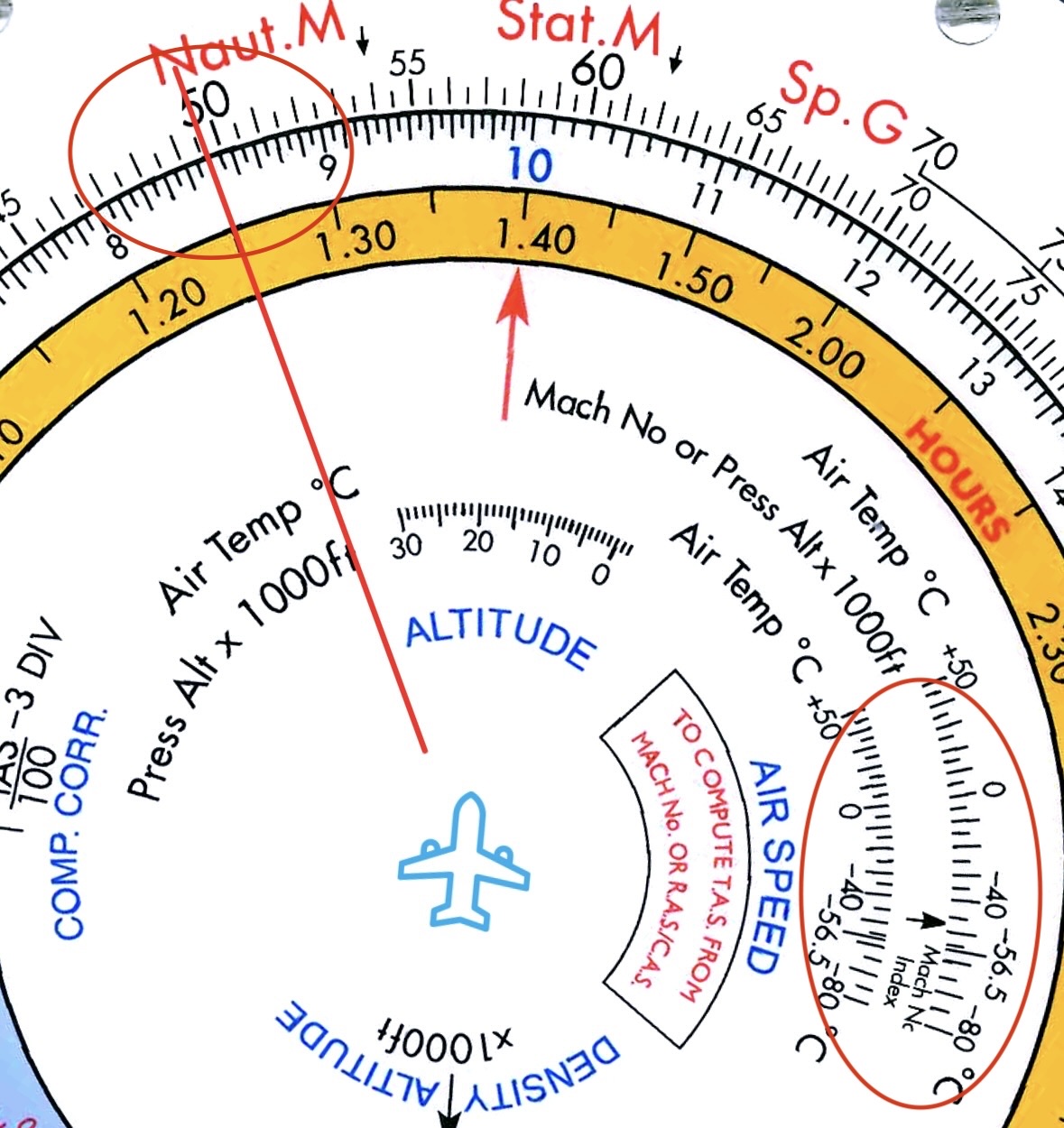
On the CRP-5 in the “AIR SPEED” window align the Mach No. Index with the Air Temp of -46.5°Ç.

On the inner-scale find Mach number 0.85 (85) and read the TAS of ±496kt on the aligned outer-scale.

Calculating Head Wind and Tail Wind component.

Trigonometry

The standard formula: Head/ Tail wind =  V×cos⁡(θ)

Where:

V = wind speed
θ = angle between the wind direction and the (runway) heading.

Apply HWC and TWC to determine GS from TAS and vice versa (061.01.05.04.02).

Explain the relationship between GS and TAS with increasing WCA (061.01.05.04.03).

Calculate GS with: mechanical computer (TOV solution), and MDR. Given track, TAS and WV (061.01.05.04.04).

Example: Given: True Course from A to B = 090°, TAS = 460 kt, W/V = 360/100 kt, Average variation = 10°E, Deviation = -2°. Calculate the compass heading and GS..

Solution:

Calculate GS and Drift:

Step 1: Using the CRP-5 set the center-dot over the TAS of 460kt.

Step 2: Set the wind-direction of 360° under the “True”-index.

Step 3: draw a wind-mark of 100kt directly under the center-dot.

Step 4: rotate the inner-ring to put the true heading of 90° under the “True”-index.

Read off a drift of 12°R.

Step 5: rotate the true heading of 90° on the inner-ring to align it with 12°R on the outer-ring.

The wind-mark is now on top of a GS of 450kt and still showing a drift of 12°R.

C	D	M	V	T	D	TTRK
70°(C)	2°L	068°(M)	10°E	078°(T)	12°R	090°(T)

Perform GS, distance and time calculations (061.01.05.04.05).

Consider the following example (although mixed learning objectives):

Example: The pilot of a light aircraft has updated the flight log and has been asked by ATC for an estimate for arrival time at RODRA.

What is (1) the average ground speed experienced in the cruise up to point TORDU (LO: 061.01.05.04.07) and (2) the new estimated time overhead RODRA (LO: 061.01.05.04.06)?

Assume the aircraft reached Top of Climb at the planned location.

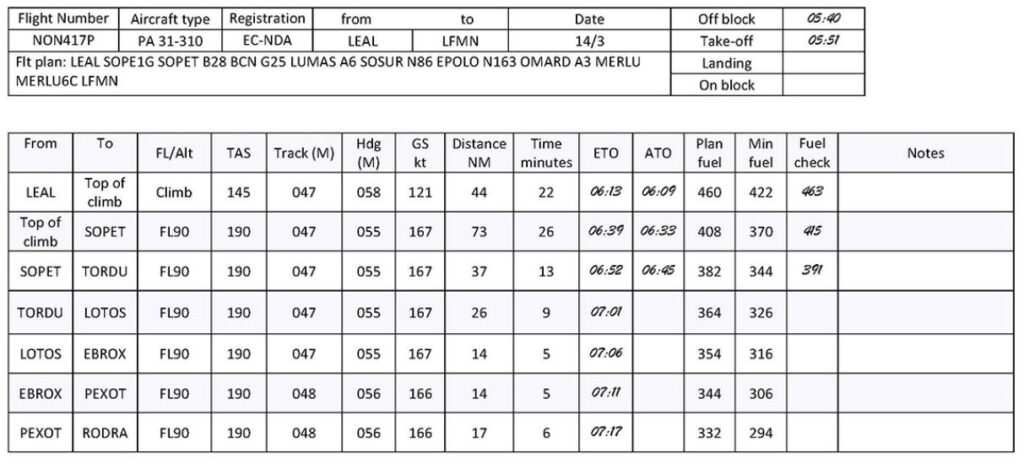
Solution

Based on the Actual Time Overhead (ATO), it took 36 minutes (06:45 – 06:09) to fly from “top of climb” to TORDU. The distance flown was 73 NM + 37 NM = 110 NM.

So the average GS from “top of climb” to TORDU was 110 NM / 36 min = 3.056 NM/min = 183 NM/h = 183 kt.

The “distance to go” from TORDU to RODRA is 26 NM + 14 NM + 14 NM + 17 NM = 71 NM.

Flying the remaining distance of 71 NM with an average GS of 3.056 NM/min will take about 23 minutes (71 / 3.056). As the actual time overhead TORDU was 06:45 and adding 23 minutes, the expected time overhead RODRA will be 07:08.

Calculate revised GS to reach a waypoint at a specific time (061.01.05.04.06).

Calculate the average GS based on two observed fixes (061.01.05.04.07).

Example: Based on the following log, what was the average Ground Speed experienced between HURLY and GISBY?

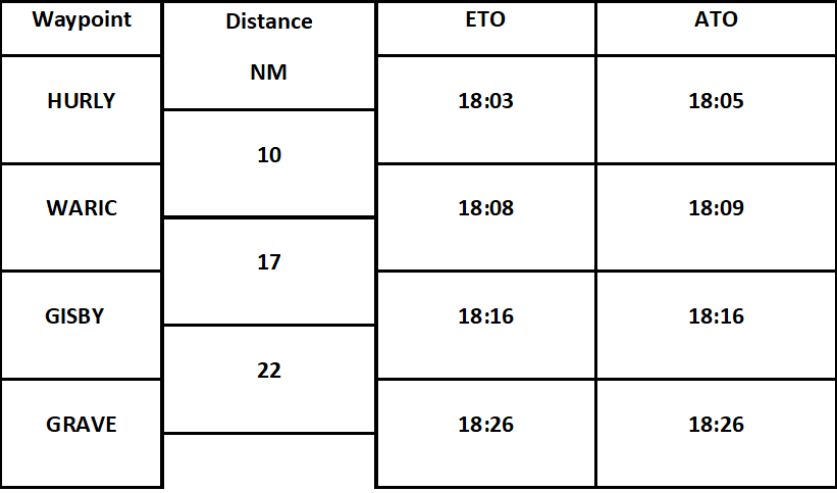
Solution:

The distance from HURLY to GISBY is 10 + 17 = 27 NM. Based on the ATO it took 18:16 – 18:05 = 11 minutes to fly from HURLY to GISBY. Therefore the average GS was 27 NM / 11 minutes = 2.45 NM/min = 147 NM/h (2.45 x 60) = 147kt .

Gradient (°) = (vertical distance (ft) / 100) / ground distance (NM)

Glide path (%) = (vertical distance (ft) / 60) / ground distance (NM)

Note: these rules of thumb are based on the assumption that 1 NM = 6000 ft.

Example 1: Your aircraft has 75 NM (track) to go to the initial approach fix, at which you should be level at 7500 feet altitude. You are cleared to descend from your present altitude of 35000 feet. What descent gradient should you achieve?

• 7.6 %
• 4.6 %
• 6.1 %
• 3.7 %

Solution:

Using the rule of thumb: Glide path (%) = (vertical distance (ft) / 60) / horizontal distance (NM)

Vertical distance = 35,000 – 7,500 = 27,500 ft
Horizontal distance = 75NM

Glide path (%) = (27,500 / 60) / 75 = 458,33 / 75 ≈ 6.1 %

Rate of Descent (ft/min) = Gradient (°) * Ground Speed (NM/min) x 100

Rate of Descent (ft/min) = Glide path (%) * Ground Speed (kt)

Vertical speed (ft/min) = (Ground Speed (kt) × gradient (ft/NM)) / 60

Example: During approach the following data are obtained: DME 12.0 NM, altitude 3000 ft DME 9.8 NM, altitude 2400 ft TAS = 160 kt, GS = 125 kt The rate of descent is:

• 700 ft/min
• 750 ft/min
• 600 ft/min
• 570 ft/min

Solution:

Using the rule of thumb:

Vertical speed (ft/min) = (125 * 600/2.2) / 60 = 568 ft/min.

If you forgot the rule of thumb:

At 12.0 NM distance of the DME the altitude is 3000 ft, 2.2 NM later (at 9.8NM of the DME) the altitude is 2400 ft. So it descended 600ft by traveling 2.2 NM over the ground.

With a ground speed of 125 kt (125 NM/h) it took the aircraft 0.0176 hour (1.056 min) to travel the 2.2 NM, therefore it descended 600ft in 1.056 min. Thus, the rate of descent is 568.18 ft/min (600/1.056).

Example: