WGS-84 ellipsoid (061.01.04.01)
State that 1 NM is equal to 1.852 km, which is the average distance of 1′ of latitude change on the WGS-84 ellipsoid. (…04.01.01)
State that 1′ of longitude change at the equator on the WGS-84 ellipsoid is approximately equal to 1 NM. (…04.01.02)
The units of distance that are used in aeronautical navigation are meters (m), kilometers (km), nautical miles (NM) and feet (ft).
A nautical mile is defined as how far you travel on Earth when you move one minute of arc (1/60 of a degree), north/south (latitude), along its surface.
1 minute (‘) of latitude change along a meridian (a circumference / great circle) is 1 nautical mile (NM).
As 1 degree (°) equals 60 minutes, 1 degree change of latitude is therefore 60NM. The circumference of the Earth is 360° x 60 NM / ° = 21.600 NM.
As the circumference of the Earth equals 40,000 km, the conversion can be derived as 1 NM = 1.852 km (40.000 km / 21,600 NM).
1 NM = 1.852 km
A parallel of latitude is not a circumference of the Earth or “great circle”. A change in longitude from, for example, 020°N to 021°N on the 45°N meridian is therefore not 60 nautical miles, but smaller. The equator however is an exception. This parallel is approximately equal to the Earth’s circumference and therefore, 1 minute (‘) of longitude change along the Equator’s parallel is equal to 1 NM.
1 minute (‘) of longitude change along the Equator’s parallel is equal to 1NM.
De afstandseenheden die in de luchtvaartnavigatie worden gebruikt, zijn meters (m), kilometers (km), nautical miles (NM) en feet (ft).
Een nautical mile is gedefinieerd als de afstand die je over de aarde aflegt wanneer je één boogminuut (1/60 graad) noord/zuid (breedtegraad) over het aardoppervlak beweegt.
1 minuut (‘) breedtegraadverandering langs een meridiaan (omtrek / grootcirkel) is 1 nautical mile (NM).
Als 1 graad (°) gelijk is aan 60 minuten, is 1 graad breedtegraadverandering dus gelijk aan 60 NM. De omtrek van de aarde is daarmee: 360° x 60 NM / ° = 21.600 NM.
Omdat de omtrek van de aarde 40.000 km is, kan de omrekening worden afgeleid als 1 NM = 1,852 km (40.000 km / 21.600 NM).
1 nautical mile = 1,852 km
Een breedtegraad is geen omtrek van de aarde of een “grootcirkel”. Een lengtegraadverandering van bijvoorbeeld 020°N naar 021°N op de meridiaan van 45°N is daarom niet 60 NM, maar kleiner. De evenaar vormt echter een uitzondering. Deze breedtegraad is ongeveer gelijk aan de omtrek van de aarde en daarom is 1 minuut (‘) lengtegraadverandering langs de evenaar wel gelijk aan 1 nautical mile.
1 minuut (‘) lengtegraadverandering langs de evenaar is gelijk aan 1 nautical mile.
Units (061.01.04.02)
Convert between units of distance (nautical mile (NM), kilometre (km), statute mile (SM), feet (ft), inches (in)). (…04.02.01)
As stated earlier the most import units of distance that are used in aeronautical navigation are meters (m), kilometres (km), nautical miles (NM) and feet (ft). However, the EASA learning objectives also require that you can convert the units Statute Mile (SM) and Inches (in).
It is useful to remember the following approximations:
| 1 NM | 1.852 km |
| 1 ft | 0.3048 m |
| 1 SM | 5280 ft |
| 1 in | 2.54 cm |
With this data, you can calculate the most important conversion. A more detailed conversion table can be found here.
This isn’t the only thing you need to remember for your ATPL exams, and mistakes are human. If you don’t remember the above conversions, the Pooleys CRP-5 computer (which you can bring to your exam) can help.
Zoals eerder vermeld zijn de belangrijkste afstandseenheden die in de luchtvaartnavigatie worden gebruikt, meters (m), kilometers (km), nautical miles (NM) en feet (ft). De leerdoelen van de EASA vereisen echter ook dat je de eenheden Statute Mile (SM) en Inches (in) kunt omrekenen.
Het is handig om de volgende benaderingen te onthouden:
| 1 NM | 1.852 km |
| 1 ft | 0.3048 m |
| 1 SM | 5280 ft |
| 1 in | 2.54 cm |
Met deze gegevens kun je de belangrijkste conversies uitvoeren. Een meer gedetailleerde omrekeningstabel vind je hier.
Nou is dit niet het enige dat je moet onthouden voor je ATPL-examens en een vergissing is menselijk. Mocht je bovengenoemde omrekeningen niet meer weten, dan biedt de Pooleys CRP-5 computer (die je mee mag nemen naar je examen) uitkomst.
Graticule distances (061.01.04.03)
Calculate the distance between positions on the same meridian, on opposite (antipodal) meridians, on the same parallel of latitude, and calculate new latitude/longitude when given distances north-south and east-west. (…04.03.01)
As stated earlier, 1 NM equals 1 minute (‘) of latitude change. The following examples show how to calculate the distance between positions on the same meridian.
Example 1: Calculate the distance between 34°15’N108°22’E and 36°00’N108°22’E along the meridian:
| 36°00’N | |
| 34°15’N | − |
| 35°45’N | (60′ – 15′) |
| 34°00’N | − |
| 01°45’N |
}
Solution:
The two locations have the same longitude (N108°22’E), so we are only dealing with a change of latitude, along a meridian, between 34°15N and 36°00N.
The two latitudes are both in the northern hemisphere, so subtract to find the change of latitude.
This results in 01°45′, which equals 105′ (60+45), which equals 105NM.
Example 2: Calculate the distance along a meridian between 65°53’N and 11°41’S:
| 65°53’N | |
| 11°41’S | + |
| 66°34’N | (53′ + 41′ = 94′, 01°34′) |
| 11°00’S | + |
| 87°34’ |
}
Solution:
In this case the locations are not in the same hemisphere, so we have to add to find the change of latitude along the meridian.
This results in 87°34’, which equals 5274′ ((87×60)+54), which equals 5274NM
Example 3: An aircraft at a latitude of 11°00’S flies north at a groundspeed of 780km/hour, what will be its latitude after 2,5 hours of flight?
}
Solution:
1NM = 1,852km. So traveling at 780km/h, equals 421,17NM/h (780 ÷ 1,852), or knots(KT).
So after 2.5 hours of flight it travelled, ≈ 1053 nautical miles (2,5×421,17).
As 1NM equals 1 minute (‘), and 1 degree (°) equals 60 minutes, it had an change of latitude of 17.55 degrees (1053 ÷ 60). 0.55° = 33 minutes (0.55×60), so in total a change of 17°33′.
The aircraft started its journey at 11°00′ in the southern hemisphere, flying north. So after 2.5 hours of flight it ends at 06°33’N (17°33′ – 11°00).
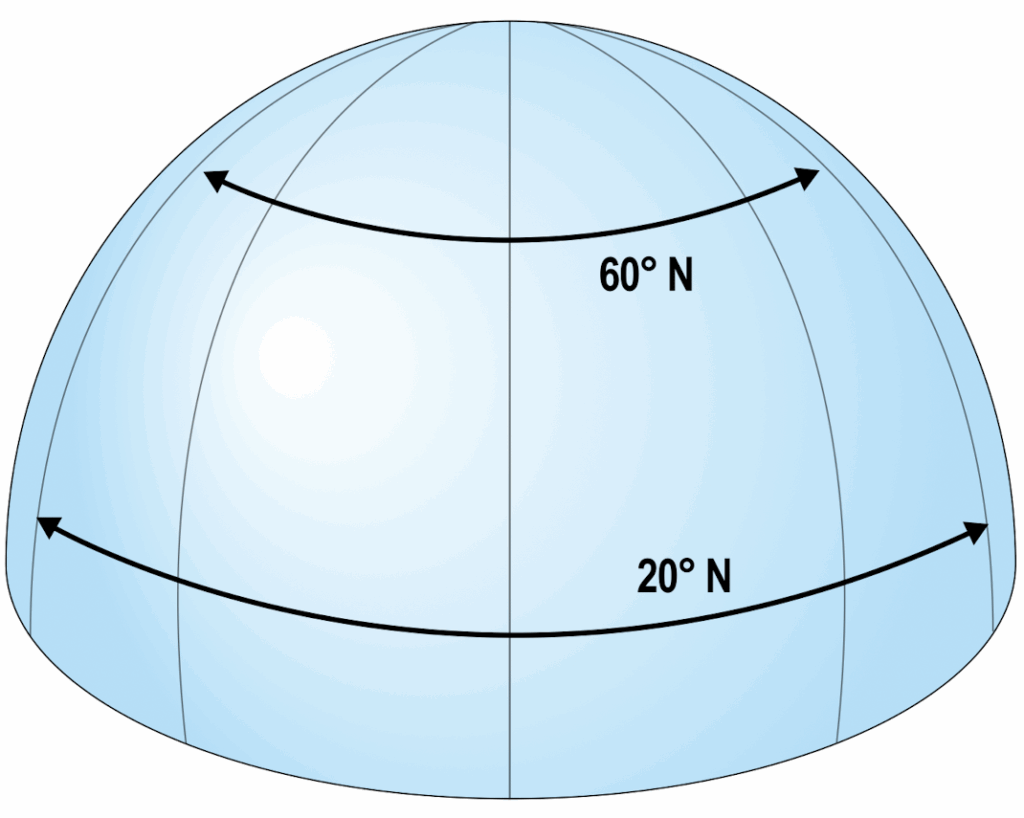The diagram shows that moving away from the equator the east/west distance decreases for the same change of longitude. The distance travelled east/west (departure) is decreasing as latitude increases, and can be calculated by using the formula:
Departure (NM) = change in longitude (‘) x cos (latitude)
Important: change in longitude in minutes (‘)
The units are important here as the formula rests on the idea that 1 NM is one minute of arc, even though the east/west distance is not along a circumference but a parallel of latitude.
Calculating departures
Example 1: Calculate the departure between 109°00’E and 108°00’W along the 34°00’S parallel:
| 109°00’E | |
| 108°00’W | + |
| 212’00′ | |
| 360°00′ | |
| 212°00’ | – |
| 148°00′ |
}
Solution:
The locations are not in the same hemisphere, so we have to add to find the change of longitude along the parallel.
The result (212°00’) is larger than 180°, so subtract from 360° to find the shorter way round, 148°00′.
We need the change in longitude in minutes!: so multiply 148° x 60 minutes/degree = 8,880′
Now using the formula: departure (NM) = change of longitude x cos(latitude) = 8,800′ x cos(34°) = 8,800′ x 0.829 ≈ 7296 NM
Example 2: Find the departure between S21°00 ‘W019°11’ and S21°00 ‘E007°29’:
| 007°29’E | |
| 019°11’W | + |
| 026’40′ |
}
Solution:
The locations are again not in the same hemisphere, so we have to add to find the change of longitude along the S21°00′ parallel.
The result (026°40’) has to be converted to minutes, (26 x 60) + 40 = 1,600′.
Now using the formula: departure (NM) = change of longitude x cos(latitude) = 1,600′ x cos(21°) = 1,600′ x 0.9336 ≈ 1494 6NM
Example 3: What is the longitude of position A, if:
- Position B: 50°00’N 036°23’E
- Departure 271 NM
- B is to the west of A
| 036°23’E | |
| 007°02’ | + |
| 043’25’E |
}
Solution:
departure (NM) = 271 NM = change of longitude x cos(50°)
Rewritten: change of longitude = 271 NM ÷ cos(50°) ≈ 422 minutes. Which equals, 7,034 degrees => 007°02′ (0,034 x 60 = 2).
It is stated that location A is east of location B, so the longitude of A should be greater, therefore adding the change of longitude to the coordinates of location B. Location A is at 50°00’N 043’25’E
Combining the both
Example 1: An aircraft departs from position A (04°10’S 178°22’W) and flies southward, following the meridian, for 2630NM. It then flies eastwards along the parallel of latitude for 281NM to position B. What are the coordinates of position B?
| 04°10’S | |
| 43°50′ | + |
| 48’00’S | |
| 178°22’W | |
| 003°08′ | – |
| 175°14’W |
}
Solution:
First calculating the change of latitude flying southward: 2630NM = 2630′ (as a meridian is circumference (great circle). Turn 2630′ into degrees: 2630 ÷ 60 = 43.833° = 43° and 50′ (0.833 x 60).
As the aircraft was flying southwards, starting in the southern hemisphere, it got further away from the equator, so adding the change of latitude to location A results in the intermediate location of 48°00’S 178°22’W.
Now it starts flying eastwards along the parallel at 48°00’S for 281NM.
Calculating the change of longitude:
Departure (NM) = 281 NM = change of longitude x cos(48°).
Change of longitude = 281 NM ÷ cos(48°) = 281 x 0.669 ≈ 188 minutes.
Convert 188′ to degrees: 188 ÷ 60 = 3.133° = 3° and 08′ (0.133 x 60).
As the aircraft was flying eastwards in the western hemisphere it was flying towards the Greenwich meridian, so subtracting the change of longitude from the intermediate location (48°00’S 178°22’W) results in the coordinates of location B: 48°00’S 175°14’W
Example 2: Again an aircraft departs from position A (04°10’S 178°22’W), but this time it flies northward, following the meridian, for 2423 NM. It then flies westward along the parallel of latitude for 510 NM to position B. What are the coordinates of position B?
| 04°10’S | |
| 40°23′ | – |
| 03’47’S | |
| 40°00′ | – |
| 37°47’N | ← -37°47’S |
| 178°22’W | |
| 006°43′ | + |
| 187°05W | |
| 187°05′ | |
| 180°00′ | – |
| 007°05′ | |
| 180°00’E/W | |
| 007°05′ | – |
| 172°55’E |
}
Solution:
The change of latitude flying northward: 2423NM = 2423′.
2423′ ÷ 60 = 40.383° = 40°23′ (0.383 x 60 = 23).
The aircraft this time is flying northward, thus flying towards the equator and passing it, so subtract.
The intermediate location is therefore at latitude -37°47’S, so flipping sides, meaning 37°47’N.
Now calculating the change of longitude based on the parallel at 37°47’N and traveling 510 NM:
Departure (NM) = 510 NM = change of longitude x cos(37.783°).
(47 minuten = 0.783 degrees (47/60))
Change of longitude = 510 NM ÷ cos(37.783°) = 510 x 0.790 ≈ 403 minutes.
Convert 403′ to degrees: 403 ÷ 60 = 6.7166° = 006° and 43′ (0.7166 x 60).
As the aircraft was now flying westward in the western hemisphere it was flying away from the Greenwich meridian, so add the change of longitude to the intermediate location (37°47’N 178°22’W), which results in a longitude of 187°05W.
CAUTION: A longitude >180° is not possible, so clearly the airplane has passed the Greenwich anti-meridian, 180°E/W, into to easterly hemisphere.
It did so by 187°05′ – 180°00′ = 007°05′
So the new longitude: 180°00’E/W – 007°05′ = 172°55’E, which means that position B is at 37°47’N 172°55’E
Zoals eerder vermeld, staat 1 NM gelijk aan 1 minuut (‘) breedtegraadverandering. De volgende voorbeelden laten zien hoe je de afstand tussen posities op dezelfde meridiaan kunt berekenen.
Voorbeeld 1: Bereken de afstand tussen 34°15’N108°22’O en 36°00’N108°22’O langs de meridiaan.
| 36°00’N | |
| 34°15’N | − |
| 35°45’N | (60′ – 15′) |
| 34°00’N | − |
| 01°45’N |
}
Uitwerking:
De twee locaties hebben dezelfde lengtegraad (N108°22’O), dus we hebben alleen te maken met een breedtegraadverandering langs een meridiaan, tussen 34°15N en 36°00N.
De twee breedtegraden liggen beide op het noordelijk halfrond, dus trek ze van elkaar af om de breedtegraadverandering te vinden.
Dit resulteert in 01°45′, wat gelijk is aan 105′ (60 + 45), wat gelijk is aan 105 NM.
Voorbeeld 2: Bereken de afstand langs een meridiaan tussen 65°53’N and 11°41’Z:
| 65°53’N | |
| 11°41’Z | + |
| 66°34’N | (53′ + 41′ = 94′, 01°34′) |
| 11°00’Z | + |
| 87°34’ |
}
Uitwerking:
In dit geval liggen de locaties niet op hetzelfde halfrond, dus moeten we optellen om de breedtegraadverandering langs de meridiaan te vinden.
Dit resulteert in 87°34′, wat gelijk is aan 5274′ ((87×60)+54), wat gelijk is aan 5274 NM
Voorbeeld 3: Een vliegtuig op een breedtegraad van 11°00’Z vliegt noordwaarts met een grondsnelheid van 780 km/uur. Wat zal de breedtegraad zijn na 2,5 uur vliegen?
}
Solution:
1 NM = 1,852 km. Dus met een snelheid van 780 km/u is dit gelijk aan 421,17 NM/u (780 ÷ 1,852), of knopen (KT).
Na 2,5 uur vliegen heeft het vliegruig dus ≈ 1053 NM (2,5 × 421,17) afgelegd.
Omdat 1 NM gelijk is aan 1 minuut (‘) en 1 graad (°) gelijk is aan 60 minuten, is de breedtegraadverandering 17,55 graden (1053 ÷ 60). 0,55° = 33 minuten (0,55×60), dus in totaal een verandering van 17°33′.
Het vliegtuig begon zijn reis op 11°00′ op het zuidelijk halfrond en vloog noordwaarts. Na 2,5 uur vliegen eindigt het dus op 06°33’N (17°33′ – 11°00).
Uit het diagram blijkt dat naarmate men verder van de evenaar komt, de oost/west-afstand afneemt bij eenzelfde verandering van lengtegraad. De afgelegde oost-westafstand (departure) neemt af naarmate de breedtegraad toeneemt en kan worden berekend met de formule:
Departure (NM) = change in longitude (‘) x cos (latitude)
Important: change in longitude in minutes (‘)
De eenheden zijn hierbij van belang omdat de formule gebaseerd is op het idee dat 1 NM gelijk is aan één boogminuut, ook al loopt de oost/west-afstand niet langs een omtrek maar langs een breedtegraad.